新闻公告
留学资讯
【优能1对1】优能名师带你备战中考:27题第一问专题训练
2017-06-13 15:48
来源:
作者:
【优能1对1】优能名师带你备战中考
27题第一问专题训练
【题型分解】
(一)点坐标与线段之间的转换
1.线段长的求法:与平行于x轴,用右点横坐标减左点横坐标;与平行于y轴,用上点横坐标减下点横坐标.
2.在平面直角坐标系内,两点A(x1,y1),B(x2,y2)的中点坐标为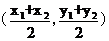 .
.
(二)由函数解析式可得到的信息
1.一次函数y=-2x+4的图象与x轴交点坐标 (2,0) ,与y轴交点坐标 (0,4) .
2.一次函数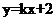 的图象与y轴交点坐标 (0,2) .
的图象与y轴交点坐标 (0,2) .
3.一次函数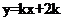 的图象与x轴交点坐标 (-2,0) .
的图象与x轴交点坐标 (-2,0) .
4.一次函数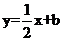 的图象与x轴夹角正切值 1/2 .
的图象与x轴夹角正切值 1/2 .
5.抛物线y=-x2+2x+3的图象与x轴交点坐标 (-1,0),(3,0) ,与y轴交点坐标 (0,3) ,顶点坐标 (1,4) .
6.抛物线y=ax2+bx+5的图象与y轴交点坐标 (0,5) .
7.抛物线y=﹣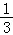 x2﹣
x2﹣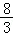 x+c的图象的对称轴 x=-4 .
x+c的图象的对称轴 x=-4 .
8.抛物线y=ax2-5ax+b的图象的对称轴 x=5/2 .
9.抛物线y=ax2-5ax-6a的图象与x轴交点坐标 (6,0),(-1,0) .
10.抛物线y=x2-(k+1)x+k的图象与x轴交点坐标 (1,0),(k,0) .
【链式习题】
1.如图,抛物线y=ax2+bx+4交x轴于A、B两点,交y轴于点C,∠CBO=45°,OB=4OA,求抛物线的解析式.

∵抛物线y=ax2+bx+4交y轴于点C,
∴C(0,4),
∴OC=4,
∵∠BOC=90°,∠CBO=45°,
∴OB=OC=4,
∴B(4,0),
∵OB=4OA,
∴OA=1,
∴A(﹣1,0),
∴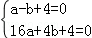 ,
,
∴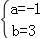 ,
,
∴抛物线解析式为y=﹣x2+3x+4.
2.抛物线y=ax2+bx-8与x轴交于A、B,与y轴交于C,D为抛物线的顶点,AB=2,D点的横坐标为3,求抛物线的解析式.
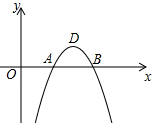
∵抛物线y=ax2+bx﹣8与x轴交于A、B,与y轴交于C,D为抛物线的顶点,AB=2,D点的横坐标为3,
∴A(2,0),B(4,0),
∴ ,
,
解得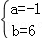 ,
,
∴抛物线解析式为y=﹣x2+6x﹣8;
3.抛物线y=-x2-(k-1)x+k(k>0)与x轴相交于A、B两点,与y轴相交于C点,该抛物线的顶点D 在第一象限,并且抛物线的对称轴与x轴相交于点E, DE=4,求这条抛物线的解析式.
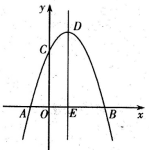
∵D为抛物线的顶点,DE=4,
∴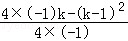 =4,
=4,
解得k1=3,k2=﹣5(舍),
∴抛物线的解析式y=﹣x2+2x+3;
4.已知开口向上的抛物线y=ax2+bx+c与x轴相交于点A、B,与y轴相交于点C,顶点坐标为(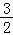 ,﹣
,﹣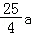 ),连接AC.若AC=
),连接AC.若AC=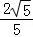 AB,求a的值.
AB,求a的值.
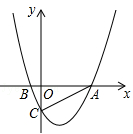
∵抛物线顶点坐标为(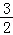 ,﹣
,﹣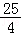 a),
a),
∴﹣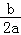 =
=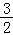 ,
,
∴b=﹣3a
∴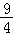 a+
a+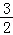 (﹣3a)+c=﹣
(﹣3a)+c=﹣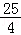 a,
a,
∴c=﹣4a
∴y=ax2﹣3ax﹣4a,C(0,﹣4a),
∴OC=4a.
当y=0时,ax2﹣3ax﹣4a=0,
∵a≠0∴x2﹣3x﹣4=0,
∴x1=4,x2=﹣1,
∴A(4,0)B(﹣1,0),
∴AB=5
∴AC=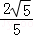 AB=2
AB=2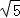 ,
,
∵∠AOC=90°,
∴OC2+OA2=AC2,
∴OC=2,
∴4a=2,
∴a=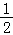 ;
;
5.在平面直角坐标中,抛物线y=ax2-3ax-10a(a>0)分别交x轴于点A、B(点A在点B左侧),交y轴于点C,且OB=OC,求a的值.
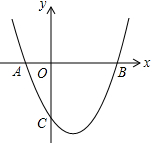
令y=0,则ax2﹣3ax﹣10a=0,
即a(x+2)(x﹣5)=0,
∴x1=﹣2,x2=5,
∴A(﹣2,0),B(5,0),
∴OB=5,
∵OB=OC,
∴OC=5,
∴C(0,﹣5),
∴﹣5=﹣10a,
∴a=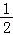 ;
;
6.在平面直角坐标系中,点0为坐标原点,抛物线y=x2-(k+1)x+k(k>1)与x轴交于点A、B(点A在点B的左侧),与y轴正半轴交于点C,点D为抛物线的顶点,抛物线的对称轴交x轴于点E.当AB=4时,求抛物线的解析式.

如图1,当y=0时,x2﹣(k+1)x+k=0,解得x=1或x=k,
∵点A在点B的左侧,k>1,
∴A(1,0),B(k,0),
∵AB=k﹣1=4,
∴k=5,
∴抛物线的解析式为:y=x2﹣6x+5;
7.如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线 y=ax2+(a-5)x+c过点B、C两点,求抛物线的解析式及顶点E的坐标.
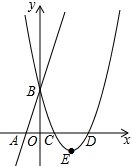
∵直线l:y=3x+3与x轴交于点A,与y轴交于点B,
∴A(﹣1,0),B(0,3),
∵A、C关于y轴对称,
∴C(1,0),
把B、C两点坐标代入 y=ax2+(a﹣5)x+c,
得到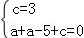 解得
解得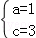 ,
,
∴抛物线解析式为y=x2﹣4x+3,
∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴顶点E(2,﹣1).
8.如图1,在平面直角坐标系中,点O为坐标原点,抛物线y=-x2+bx+a与x轴相交于点A、点B(点A在点B的左侧),与y轴正半轴相较于点C,直线y=kx-3k经过点B、C两点,且△BOC为等腰直角三角形,求抛物线的解析式.
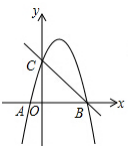
如图1,
令y=0,得kx﹣3k=0,
∵k≠0,
∴x=3,B(3,0).
∵△BOC是等腰直角三角形,∠BOC=90°,
∴OB=OC=3,
∴C(0,3).
∵y=﹣x2+bx+a经过点B、C,
∴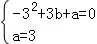 ,
,
∴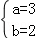 ,
,
∴抛物线的解析式为y=﹣x2+2x+3;
9.如图,在平面直角坐标系中,O为坐标原点,直线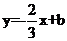 与x轴交于点B,与y轴交于点C,抛物线y=ax2-5ax-6a(a<0=经过B、C两点,与x轴交于另一点A,求a,b的值.
与x轴交于点B,与y轴交于点C,抛物线y=ax2-5ax-6a(a<0=经过B、C两点,与x轴交于另一点A,求a,b的值.
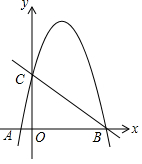
∵抛物线y=ax2﹣5ax﹣6a=a(x2﹣5x﹣6)=a(x+1)(x﹣6),
∴x1=﹣1,x2=6,对称轴x=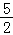 ,
,
∴A(﹣1,0),B(6,0),
∵直线y=﹣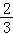 x+b与x轴交于点B,
x+b与x轴交于点B,
∴0=﹣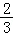 ×6+b,
×6+b,
∴b=4,
∴直线y=﹣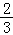 x+4,
x+4,
∴C(0,4),
∴a×(﹣1)×6=4,
∴a=﹣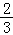 ,
,


新东方哈尔滨学校官方微信:新东方哈尔滨学校(微信号:xdfhebxx)
最新活动公告、课程优惠、考试资讯,请扫一扫二维码,关注我们的官方微信!
版权及免责声明
①凡本网注明"稿件来源:新东方"的所有文字、图片和音视频稿件,版权均属新东方教育科技集团(含本网和新东方网) 所有,任何媒体、网站或个人未经本网协议授权不得转载、链接、转贴或以其他任何方式复制、发表。已经本网协议授权的媒体、网站,在下载使用时必须注明"稿件来源:新东方",违者本网将依法追究法律责任。
② 本网未注明"稿件来源:新东方"的文/图等稿件均为转载稿,本网转载仅基于传递更多信息之目的,并不意味着赞同转载稿的观点或证实其内容的真实性。如其他媒体、网站或个人从本网下载使用,必须保留本网注明的"稿件来源",并自负版权等法律责任。如擅自篡改为"稿件来源:新东方",本网将依法追究法律责任。
③ 如本网转载稿涉及版权等问题,请作者见稿后在两周内速来电与新东方网联系,电话:010-60908555。
新闻公告
留学资讯